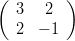Let's consider these equations
1.)this equation describe a set of points in a 3-D space. More specifically, it appears as a plane.

2.)this equation describe another set of points in a 3-D space too.

3.) this two equations describe a new set of points in space. More specifically, "it" together appears upon us as a line, rather than two isolated planes.

4.) If there is a new equations such that the unknowns can be solved.
Then these equations becomes in a way:

Are those equations same as before? What are the meanings of them?
The answer is no for the latter two. They are NEW sets of points in a 3-D space (geometrically planes) by each of them independently.
All three of them together are described as, merely, ONE point in space.